Some Algebra 1 ive need some help on solve this system of equations by using the substitution method 5x3y=11 (1) and 3x22y=1 (2)The first linear equation is 2xy = −5 2 x y = − 5 The second linear equation is 3x−y= −10 3 x − y = − 10 Add the both given See full answer belowSolve by Substitution Calculator Step 1 Enter the system of equations you want to solve for by substitution The solve by substitution calculator allows to find the solution to a system of two or three equations in both a point form and an equation form of the answer Step 2 Click the blue arrow to submit
The Elimination Method
3x y=10 x-y=2 substitution method
3x y=10 x-y=2 substitution method- x 2y 5 3x 2 3y 10 solve by elimination method Mathematics TopperLearningcom dzs9yv22 Starting early can help you score better!Solve the system of equations using the substitution method y=−3x7 x=−2y−16 Enter your answers in the boxes x= y= 2 See answers p71f2z p71f2z Y=3x7 Set it to equal 0 3x7=0 Solve (Get x by itself) 7 7 3x=7 /3 /3 x= 7/3 Same thing for other one thanks fam np BTW I'm in 8th grade and taking algebra 1 if you wanted to




2x Y 2 X 3y 15 By Elimination Method
Y=3x y=6x9 in substitution method 2 See answers taskmasters taskmasters The two equations given in the question are y = 3x And y = 6x 9 Let us now substitute the value of y from the first equation to the second equation, we get y = 6x 9 3x = 6x 93x 6x = 9 9x = 9 Multiplying both sides of the equation by 1 we getUse the substitution method to solve the system of equations 2x y = 10 3x 2y = 8 Solve the following linear system of equations using substitution Y=3x5 Y=2x6Substitution Method in Algebra!HELP PLZ!
2 Substitution method xy=16 and y=3x 3 Solve the system by the substitution method y= 2x 7 and 2x 3y = 19 4 xy= 1 and xy= 5 Solve the system by the addition method 5 Solve the system by the addition method 4x13y= 8 and 2x13y=4 6 Solve the system by graphing 3x2y=12 and x 2y= 4Substitution Method xy = 5 and 2x3y = 4LinkedIn Profilehttps//wwwlinkedincom/in/arunmamidi8ba/FaceBookhttps//wwwfacebookcom/arunkumarm144Solution Solution provided by AtoZmathcom Substitution Method Solve Linear Equation in Two Variables Solve linear equation in two variables 1 12x 5y = 7 and 2x 3y 5 = 0 2 x y = 2 and 2x 3y = 4 3 7y 2x 11 = 0 and 3x y 5 = 0
Start with the given system of equations Start with the second equation Move onto the first equation Plug in Combine like terms on the left side Subtract from both sides Combine like terms on the right side Divide both sides by to isolateThe substitution method is one way of solving systems of equations To use the substitution method, use one equation to find an expression for one of the variables in terms of the other variable Then substitute that expression in place of that variable in the second equation You can then solve this equation as it will now have only one variable(Type an ordered pair) algebra solve using the elimination method show your work if the system has no solution or an infinite number of solutions, state this xy=10 xy=2 College Algebra Solve using the elimination method




2x Y 2 X 3y 15 By Elimination Method




Each De In Problems 1 14 Is Homogeneous In Problems Chegg Com
9 solve by the substitution method 7mn= m3n=28 answer is an ordered pair 10 solve by the substitution method 3x=4y=16 3xy=26 answer is an ordered pair 11 solve by the substitution method 7 read moreSolve The Following Pair Of Linear Equation By Substitution Method 2x Y 2 And X 3y 15 Brainly In For more information and source, see on this link https//brainlyFor an answer to have an infinite solution, the two equations when you solve will equal #0=0# Here is a problem that has an infinite number of solutions #3x2y= 12# #6x4y=24# If you solve this your answer would be #0=0# this means the problem has an infinite number of solutions For an answer to have no solution both answers would not




Substitution Method



How Do You Solve The System X Y 6 And X Y 2 By Graphing Socratic
Step 1 Solve one of the equations for either x = or y = Since the coefficient of y in equation 2 is 1, it is easiest to solve for y in equation 2 Step 2 Substitute the solution from step 1 into the second equation Step 3 Solve this new equation ( for x ) Step 4 Solve for the second variable0 votes 1 answerPlease watch "Abhishek Medly 6 Zack Knight " https//wwwyoutubecom/watch?v=osa3Alk2SBM ~Hi Guys!




Ch4 Systems Of Linear Equations Y X Y X Y X Y X 3 Consistent Y 2 3 X 2 Independent Equations One Solution X Y Y X 3 Y X 2 Inconsistent Ppt Download



1
Solve by Substitution // Solve equation 2 for the variable y 2 y = 3x 1 // Plug this in for variable y in equation 1 1 (3x1) 2x = 11 1 5x = 10 // Solve equation 1 for the variable x 1 5x = 10 1 x = 2 // By now we know this much y = 3xSolve by using the substitution method {eq}y=3x2, \ x=4 {/eq} Substitution Method The substitution method is one of the techniques used for solving a system of equations The value of a2xy=10 Geometric figure Straight Line Slope = 4000/00 = 00 xintercept = 10/2 = 5 yintercept = 10/1 = Rearrange Rearrange the equation by subtracting what is to
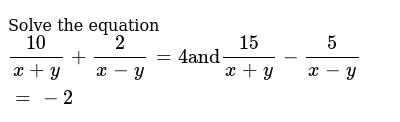



Solve The Simultaneous Equations 10 X Y 2 X Y 4 15



Solved Can I Get Someone To Answer These Using The Substi Chegg Com
Here, we have a quadratic and a linear equation which can be solved by the substitution method From the second equation, know y = 3x8 put this in place of y in the first equation We get, 3x 8 = x^22 Rearrange x^2 3x 10 = 0 It can be factorized x^2 5x 2x 10 =0 x(x5) 2(x5) = 0 (x5)(x2) = 0 Therefore, x =5 and x = 2 are the roots of equation(a) 2x 3y = 12(i) and x y = 1(ii) (ii)×3 ==> 3x 3y = 3(iii) Now we can eliminate y by adding (i) & (iii) (i) (iii) ==> 5x = 15 so x=3Take y's value from either eq 1 or 2 and plug it into the equation you didnt pick from for every value of y I pick y's value from eq 1 which is 3x10, and will plug that into eq 2 subtracted x and added 10 to both sides now take x's found value and plug it into either eq I choose eq 2




Solve The Following Pairs Of Equations By Reducing Them To A Pair Of Linear Equations Frac 10 X Y Frac 2 X Y 4 Frac 15 X Y Frac 5 X Y 2 Snapsolve



Solve Each System By The Substitution Methos X Y Chegg Com
Solve the following pair of linear equations by the substitution method (3x)/2 (5y)/3 = 2, x/yy/2 = 13/6 CBSE CBSE (English Medium) Class 10 Question Papers 6 Textbook Solutions Important Solutions 3111 Question Bank Solutions 334 Concept Notes &I'm Abhishek and today uploaded a new sum videoIThe simultanous equation calculator helps you find the value of unknown varriables of a system of linear, quadratic, or nonlinear equations for 2, 3,4 or 5 unknowns A system of 3 linear equations with 3 unknowns x,y,z is a classic example This solve linear equation solver 3 unknowns helps you solve such systems systematically




Find X And Y If I X Y 7 0 2 5 And X Y 3 0 0 3




Solve The System Of Equations Frac X 2 Y 0 8 And Frac 7 X Y 2 10 And Also Find The Value Of Frac X Y Snapsolve
Transcript Ex 33, 1 Solve the following pair of linear equations by the substitution method (i) x y = 14 x – y = 4 x y = 14 x – y = 4 From equation (1) x y = 14 x = 14 – y Substituting value of x in equation (2) x – y = 4 (14 – y) – y = 4 14 – y – y = 4 14 – 2y = 4 –2y = 4 – 14 –2y = –10 y = (−10)/(−2) y = 5 Putting y = 5 in (2) x – y = 4 x = y 4 xSo, the major difference between the substitution and elimination method is that the substitution method is the process of replacing the variable with a value, whereas the elimination method is the process of removing the variable from the system of linear equations Substitution Method Examples Example 1 Solve 2x 3y = 9 and x – y = 3Click here👆to get an answer to your question ️ Solve each pair of equation by using the substitution method x 6y = 6 3x 8y = 5




3x Y 10 And X Y 2 Problem Set 1 Q3 5 Of Linear Equations In Two Variables Youtube




X Y X Y 10 Solve The Following Brainly In
8y = 40 y = 5 Solution x = 3, y = 5 5)The system of equations are 7x 2y = 19 and x 2y = 21 From second equation x = 2y 21 Find the value of y by substituting 2y 21 for x in the first equation 7 ( 2y 21) 2y = 19 14y 147 2y = 19 12y = 128 x y = 21 x=y2 3x – 2y = 162 Substitute x=y2 in equation 2 3x – 2y = 16 3×(y2)2y=16 3y62y=16 y6=16 y=166 y=10 Substitute y=10 in eqution 1 x y = 2 x10=2 x=210 x=12 Hope it helps you If it helps you mark as brainlistUse the Substitution method to solve the system of equations 3x y = 5 4x 7y = 10 multiply first equation by 4 multiply second equation by 3 thus both equations have same x or y value in this case it is the x value 12x 4y = 12x 21y = 30



Suppose That X Y And Z Are Positive Integers Such That Xy 6 Xz 10 And Yz 15 What Is The Value Of Xyz Quora




10 X Y 5 X Y 5 6 X Y 9 X Y 6 Find Value Of X Y X Y Brainly In
3xy=23 x/3y/4=4 By Substitution 4/x9/y=5 7/x12/y= I did not understood how to solve this How to solve By substitution method solve the following simultaneous linear equantion by substiution method 4x 3y = 11 6x 7y = 5 P,Q,R have a total of ₹ 130 with themClick here👆to get an answer to your question ️ Solve 3x 4y = 10 and 2x 2y = 2 by substitution method Join / Login > 10th > Maths > Pair of Linear Equations in Two Variables Solve 3 x 4 y = 1 0 and 2 x − 2 y = 2 by substitution method Easy Answer By substitution method, 3Hence, the given pair of equations has infinite possible solutions and the relation between these variables can be given by y = 3x 3 Therefore, one of its possible solutions is x = 1, y = 0 Concept Algebraic Methods of Solving a Pair of Linear Equations Substitution Method




Ncert Class 10 Mathematics Chapter Wise Questions And Answers And Solutions




Solve By Reducing Them To A Pair Of Linear Equations 10 X Y 2 X Y 4 15 X Y 5 X Y 2 Youtube
Solving system of equation by substitution method, involves solving any one of the given equation for either 'x' or 'y' and plugging that in the other equation and solve that equation for another variable Example 1 2xy=1 3x5y=2 Solution In the given two equations, the first equation has only 'y' term So let us solve for y in the firstQuestion 1 Solve the following pair of linear equations by the elimination method and the substitution method x y =5 and 2x –3y = 4 3x 4y = 10 and 2x – 2y = 21 3x7y10=0 2 y2x3=0 Equations Simplified or Rearranged 1 3x 7y = 10 2 2x y = 3 Graphic Representation of the Equations 7y 3x = 10 y 2x = 3 Solve by Substitution // Solve equation 2 for the variable y 2 y = 2x 3 // Plug this in for variable y in equation 1




Systems Of Equations With Substitution 2y X 7 X Y 4 Video Khan Academy




Solve X Y 3 And 3x 2y 10 By Substitution Method Brainly In
6y3=39x = 13 x 2y = 1 (2) = = 15x 0 = 15 15x = 15 = x = 1 Let find the value of y x y = 7 1 y = 7 the number was x ,y is 1,6 y = 6 The original number is 16 Exercise 105 1 The sum of two number is 109 and the difference of the same numbers 29 find the numbers 2 Two number are such that the first number plus three times the second number is 1Finite Math Solve by Substitution x2y=10 , 2xy=10 , x2y=10 x − 2y = −10 x 2 y = 10 , 2x y = 10 2 x y = 10 , x 2y = −10 x 2 y = 10 Add 2y 2 y to both sides of the equation x = −10 2y x = 10 2 y 2xy = 10 2 x y = 10 x2y = −10 x 2 y = 10 Replace all occurrences of x x with −102y 10 2 y in eachSteps for Using the Substitution Method in order to Solve Systems of Equations Solve 1 equation for 1 variable (Put in y = or x = form) Substitute this expression into the other equation and solve for the missing variable Substitute your answer into the first equation and solve Check the solution



Solve The Following System Of Linear Equations Graphically 3x Y 11 0 X Y 1 0 Sarthaks Econnect Largest Online Education Community



100以上 Solve By Substitution Method X Y 14 X Y 4 Solve By Substitution Method X Y 14 X Y 4
Solve the following pairs of linear equations by the elimination method and the substitution method (i) 3x5y4=0 and 9x=2y7 asked in Mathematics by sforrest072 (128k points) pair of linear equations in two variables;The answer to these simultaneous equations is x = 1, y= 1 These two values make both equations true You can probably figure this out just by examining the two equations However, there are several other ways to find the solution One is called tFree system of equations substitution calculator solve system of equations unsing substitution method stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y




Solve The Following Pair Of Linear Equation By Substitution Method I X Y 2 3x 2y 16 Brainly In
Exercise 34 pair linear equations two variables chapter 3 NCERT solution Class 10 NCERT solutions that you will not find anywhere else!Avail 25% off on study pack Solve by substitution method 3x 4y = 10, 2x 2y = 2 By substitution method, 3 x 4 y = 1 0 & 2 x − 2 y = 2 ⇒ 2 (x − y) = 2 ⇒ x − y = 1 ___ (2) ∴ x = y 1 → (1) Substituting in equation (2) ∴ 3 x 4 y = 1 0 ⇒ 3 (y 1) 4 y = 1 0 ⇒ 3 y 3
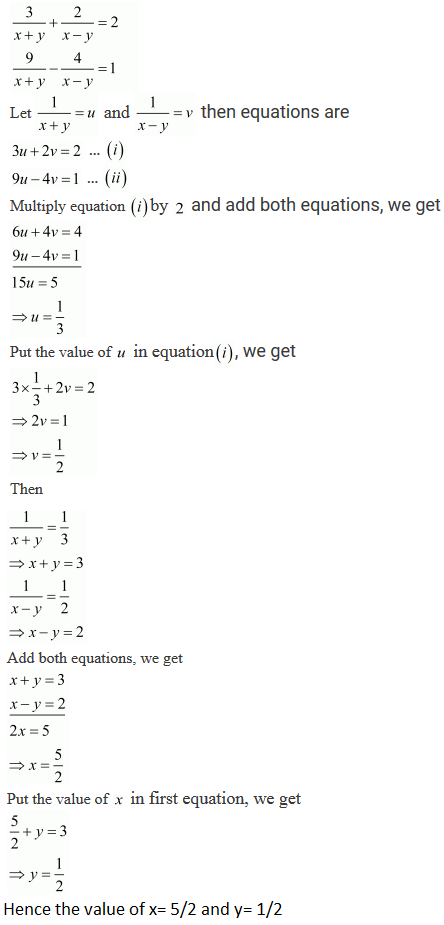



R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




Solved X2 Y 10 3x Y 10 1 Solve The System By Substitut Chegg Com
SUBSTITUTION METHOD EXAMPLES The following steps will be useful to solve the systems of linear equations using substitution Step 1 In the given two equations, solve one of the equations either for x or y Step 2 Substitute the result of step 1 into other equation and solve for the second variable Step 3So that it's less likely that we get shown up by talking birds in the future, we've set a little bit of exercise for solving systems of equations with substitution And so this is the first exercise or the first problem that they give us 3x4y=2 and y=2x5 So let me get out my little scratch pad and let me rewrite the problemSolve by the substitution method 7x 2y = 19 5x y = 33 What is the solution of the system?



Solved Find The Common Solution Of Each Using The Elimination And Substitution Method 2x Y 2 X 3y 36 B Course Hero




3x Y 10 X Y 2 Solve By Cramers Rule Brainly In
Solve the system using the substitution method y=5x2 3xy=13 Answered by a verified Math Tutor or Teacher We use cookies to give you the best possible experience on our website By continuing to use this site you consent to the use of cookies on your device as described in our cookie policy unless you have disabled them




10 X Y 2 X Y 4 15




If 3x 2y 10 And 2x 3y 15 Find The Value Of X Y Youtube




Ex 3 6 1 Vii And Viii Class 10 Ncert Solutions Maths



Q Tbn And9gcsfztjretzfhrufhn2vvzlegsmmexxszfnttwkfemhx Q3xlfdr Usqp Cau




10 X Y 2 X Y 4 15 X Y 9 X Y 2 By Substitution Method Brainly In




1 Solve The Following Systems Of Linear Equation Gauthmath




3x Y 10 X Y 2 Solve By Using Equating Coefficient Method Brainly In




Solve X And Y X 6 Y 4 1 And 3x 4 X Y 2 7 4 Related Substitution Method Pair Of Linear Equations In Two Variables Edurev Class 10 Question



Solve The Following Systems Of Equations X 2 Y 0 8 Sarthaks Econnect Largest Online Education Community




Solve The Following Simultaneousequations3x Y 10 X Y 2 Brainly In




X Y 6 X Y 2 By Elimination Method Novocom Top




J19




Ex 3 3 Qno 1 1 Solve The Pair Of Linear Equations X Y 14 X Y 4 By Substitution Method Class 10 Youtube



印刷 X Y 7 3x Y 1 Graphical Method X Y 7 3x Y 1 Graphical Method




3x Y 10 X Y 2 Solve Graph Method Brainly In




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3
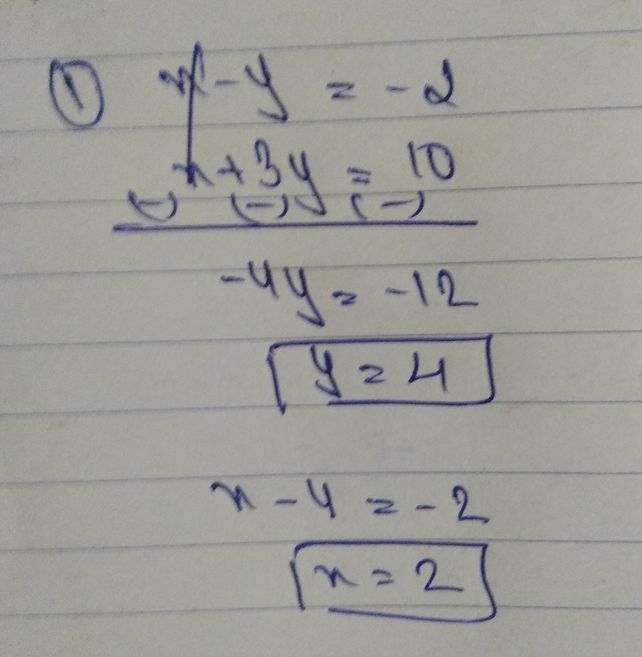



X3y10 X Y 2 2x Y 6 Xy3 X2y18 See How To Solve It At Qanda




Solve The Simultaneous Equations 10 X Y 2 X Y 4 15
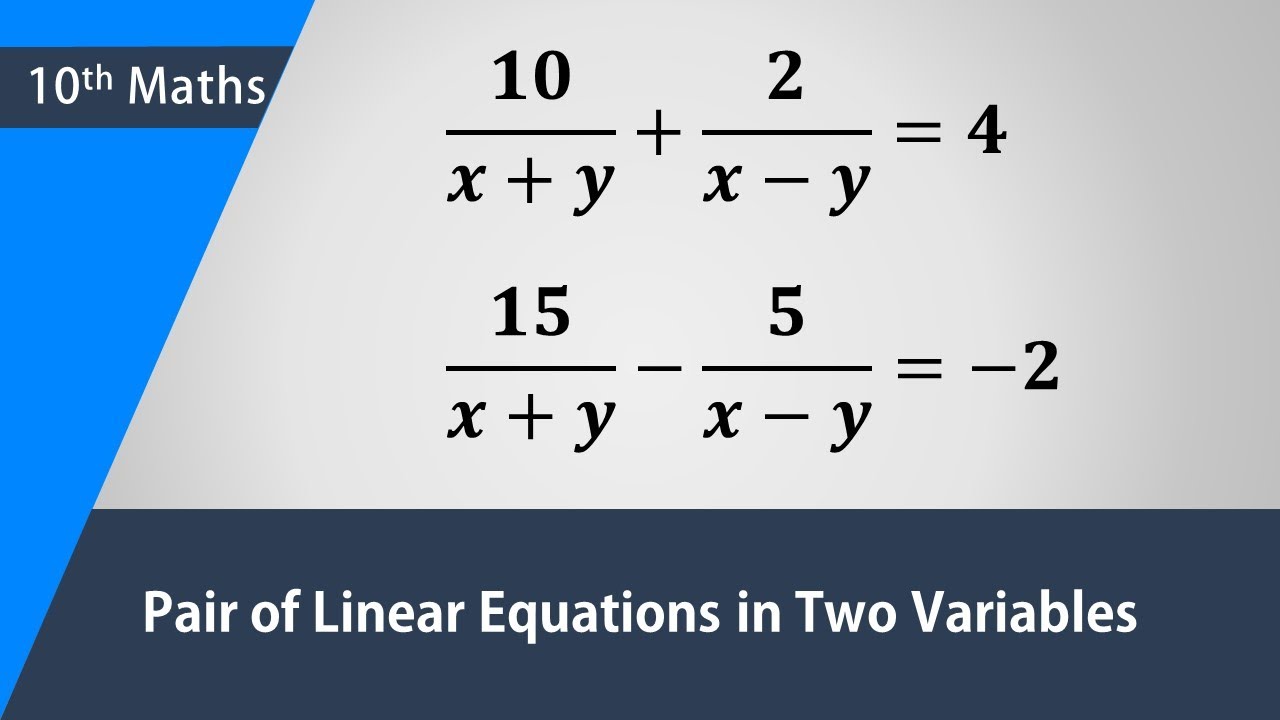



10 X Y 2 X Y 4 15 X Y 5 X Y 2 Solve For X And Y Youtube




Practical Exercises 3 System Analysis



Solve The Following Systems Of Equations Graphically X Y 6 X Y 2 Sarthaks Econnect Largest Online Education Community



Solve The Following Simultaneous Equations Using Cramer S Rule I 3x 4y 10 4x 3y 5 Sarthaks Econnect Largest Online Education Community



1




Y X 0 5 2 X 2 4 Novocom Top




X3y10 X Y 2 2x Y 6 Xy3 X2y18 See How To Solve It At Qanda



Systems Of Linear Equations




Solve 3x 4y 10 And X Y 1 Brainly In




Solve For X And Y 40 X Y 2 X Y 5 And 25 X Y 3 X Y 1 Mathematics Topperlearning Com Idbi1itt




3x Y 10 X Y 2 Solve Graph Method Brainly In
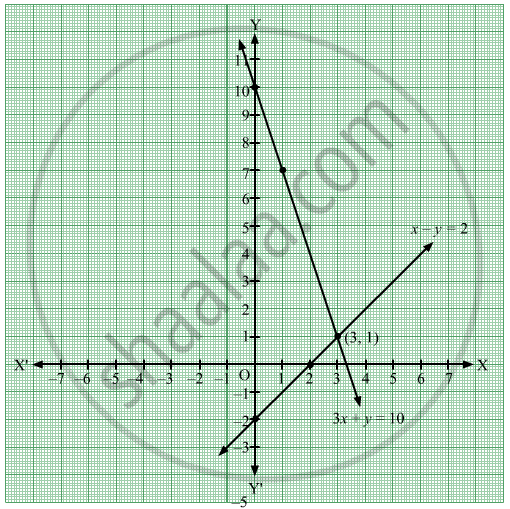



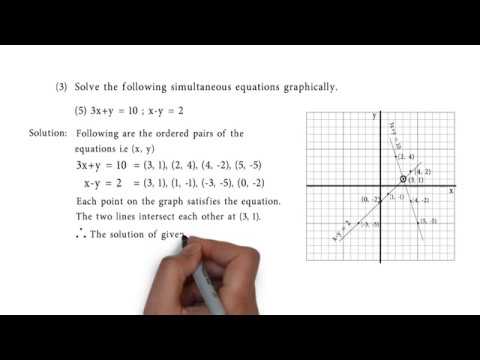
Solve The Following Simultaneous Equation Graphically 3x Y 10 X Y 2 Algebra Shaalaa Com




Solve By Substitution Method X Y 2 3x 2y 16 Brainly In



How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora




For A Pair Of Equations 2x 3y 10 And 3x Y 4 Find X




Q3e 3x Y 10 X Y 2 Solve The Following Simultaneous Equation Graphically




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3
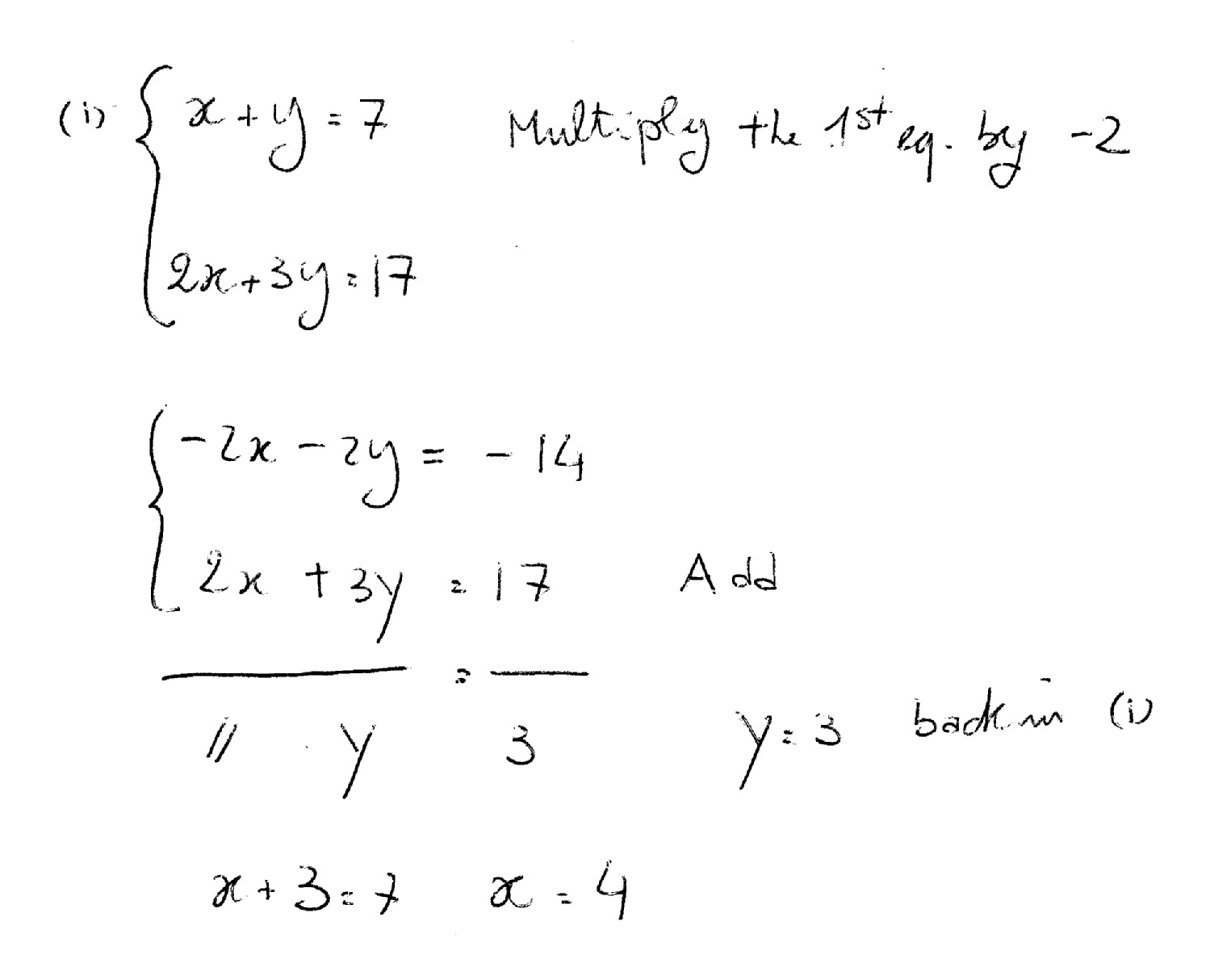



How Do You Solve The System Using The Elimination Method For X Y 7 And 2x 3y 17 Socratic



3x Y 10 And X Y 2 Problem Set 1 Q3 5 Of Linear Equations In Two Variables Youtube



The Elimination Method




Solve The Following System Of Equations 27 X Y 15 X Y 2 And 30 X Y 1 X Y 3 Mathematics Topperlearning Com X68shsoo




Solve X Y 7 And 3x 2y 11




Solve The Following System Of Equations X 2 Y 0 8 7 X




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3



The Substitution Method



16 X Y 2 X Y 1 8 X Y 12 X Y 7 Find The Value Of X And Y Quora




Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 3




Solve Each System Of Linear E See How To Solve It At Qanda



If X Y 3 X Y 1 Then What Is X Y Quora




6 2 Solving Systems Of Linear Equations 455 We Have Chegg Com




If X Y 7 Xy 10 Then The Value Of X 2 Y 2 Is X 2 Y 2 29 Youtube




Answered 7 Y 9 Xy Y Vx 11 Xy 2y X X 0 Bartleby




X Y 10 X Y 2 Cross Multiplication Elimination Substitution Brainly In




Solve The Following Systems Of Linear Equations By Chegg Com




If Math X Y 10 Math And Math X Y 12 Math Then What Are The Possible Values Of Math X Math And Math Y Math Quora




X 2 Y 0 8 7 X Y 2 10 Novocom Top




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




Express Y In Terms Of X In The Expression 3x 7y 10



How To Solve Using The Gauss Elimination Method Y Z 2 2x 3z 5 X Y Z 3 Quora



What Is The Value Of X And Y If Xy 10 And X Y 3 Quora
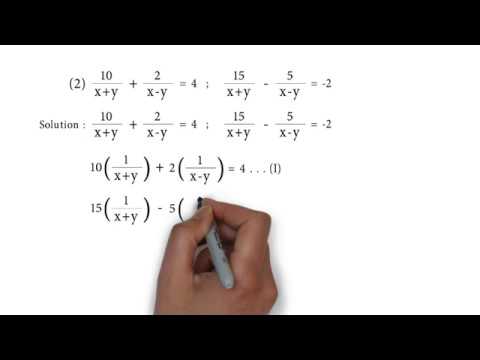



10 X Y 2 X Y 4 And 15 X Y 5 X Y 2 P S 1 4 Q2 Linear Equation In Two Variables Youtube
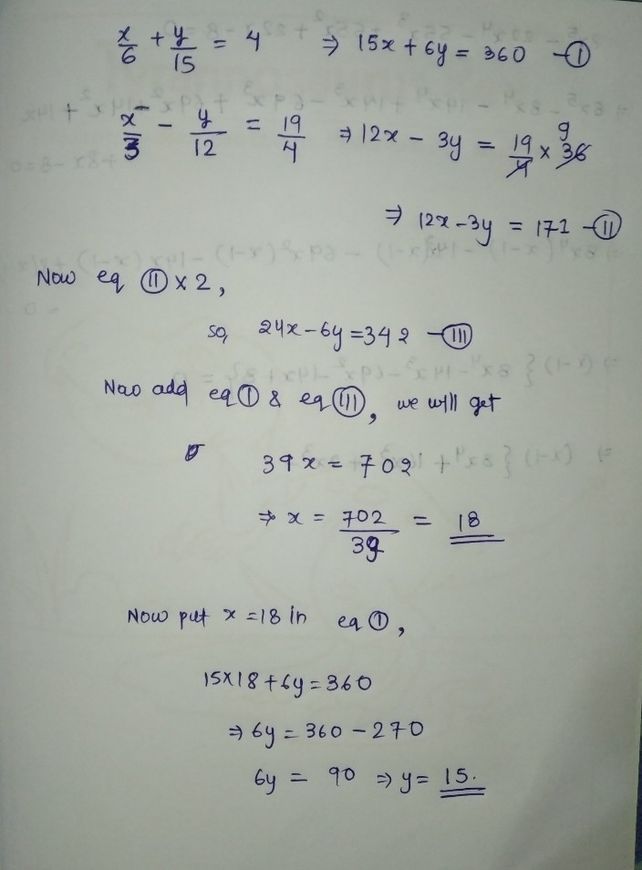



Rate 1009simultaneouslin See How To Solve It At Qanda



Maths Guru Please Help Me Solve This Simultaneous Equations For My Young Photo Education 2 Nigeria




X Y 3 And 3x 2y 10 By Substitution Method Maths Pair Of Linear Equations In Two Variables Meritnation Com
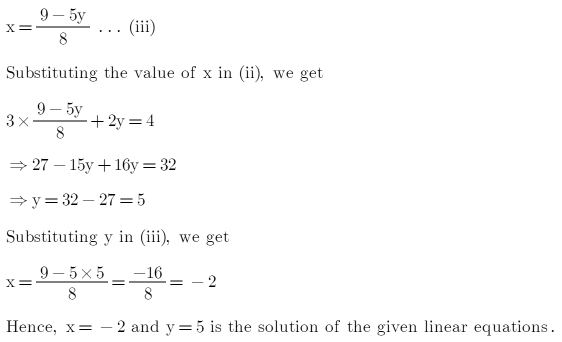



By The Substitution Method Solve The Linear Equation That Is 8 X 5 Y Is Equal To 9 And 3 X 2 Y Is Equal To 4 Mathematics Topperlearning Com Usvpr6ll




Hw 3 Due 9 27 Solve Each System Of Equations Chegg Com




Ex 3 6 1 Vii And Viii Class 10 Ncert Solutions Maths



Solve The Following Systems Of Equations 3 X Y 2 X Y 2 9 X Y 4 X Y 1 Sarthaks Econnect Largest Online Education Community



If X Y 10 And X Y 16 What Is The Value Of X Quora




Chapter 9 Systems Of Linear Equations Pdf Free Download




Ex 3 2 4 Which Of The Pairs Of Linear Equations Are Ex 3 2




Please Solve Using Elimination Method Mathematics Topperlearning Com 5a5ymyhh




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3




Ex 12 1 5 Maximise Z 3x 2y Subject To X 2y 10



1




Solve The Following Systems Of Equations By Using The Method Of Substitution 1 X Y 10 X Y 62 X Brainly In



0 件のコメント:
コメントを投稿